Простите числа изглеждат привидно случайно разпределени сред другите числа, които имат делители, но се оказа, че не са толкова разбъркани, колкото се смяташе досега.

Нов анализ на изследователите от Университета Принстън разкри скритите модели, които имат някои подобни на кристали материали.

Изследователите откриват изненадващо сходство между последователността от прости числа в дълги участъци на числовата ос и модела на резултатите от осветяването с рентгенови лъчи на материал, разкриващо вътрешното разположение на неговите атоми.

Анализът може да доведе до прогнозиране на простите числа с висока точност, твърдят изследователите. Това има връзка с една от математическите „Задачи на хилядолетието”, за чието решение Институтът Клей дава един милион долара.

Проучването е публикувано в списание Journal of Statistical Mechanics:Theory and Experiment.

"Ние показахме, че простите числа се държат почти като кристал или по-точно, като кристално подобните материали, наречени квазикристали", отбелязват Салваторе Торквато (Salvatore Torquato), професор по естествени науки и химия в Принстънския институт за наука и технология на материалите. 

В сравнение с типичните кристали квазикристалите показват по-сложно подреждане на върховете на Браг. Когато преминават през кристали, рентгеновите лъчи се отразяват от атомните равнини в посоки, определени от закона на Браг. Пиковете в типичните кристални форми са на равномерни интервали с празнини между тях. В квазикристалите между двата избрани върха на Браг попада друг връх на Браг.

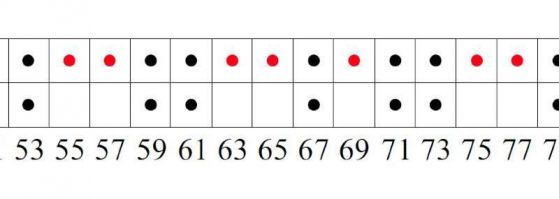
^{Изследователи от Принстън откриват сходство между моделите на атомите в някои кристално подобни материали и простите числа. Тук червените точки обозначават непростите числа, а черните точки означават просто  или "атом". Кредит: S Torquato et al. Uncovering multiscale order in the prime numbers via scattering, Journal of Statistical Mechanics: Theory and Experiment (2018).} 

Квазикристалите са структури, подобни на кристалите, но тяхната симетрия не се получава с транслиране - моделите на подредбата на атомите им никога няма да се повтарят. 

Чрез преместване на част от кристала във всяка посока можем да стигнем до друг, идентичен участък, но същото не е вярно за квазикристала - в него можем да видим в други симетрии, като петоъгълна ротационна симетрия. 

Простите числа са числа, които могат да се делят само на себе си и на единица.

Много големите прости числа са градивни елементи на много криптографски системи.

Простите числа се разполагат сякаш произволно по числовата ос, макар че математиците виждат някаква подредба.

Първите няколко примера са 2, 3, 5, 7 и 11, като стават по-редки с напредването по числовата линия.

Торквато и колегите му установяват, че когато се изследват големи поредици от числовата ос, простите номера са по-подредени от предполаганото досега, като попадат в рамките на клас от модели, известни като "хипереднаквост" (hyperuniformity).

Този странен модел е открит в разнообразни ситуации  - от клетките на ретината на птиците, в метеоритни минерали до крупномащабната структура на Вселената, наблюдавана за първи път в началото на 2000 г.

Кейти Спейлдинг (Katie Spalding) от IFLScience обяснява този модел на привидно случайно разхвърляни неща, в които има скрита подреденост, по следния начин. Пред представете си например пакетче микс от ядки от магазина и можете да видите как от случайни вибрации и разклащания частиците от само себе си се подреждат като си запълват всяко ъгълче и пролука почти перфектно. Подобна техника  обяснява резултата на екипа на Принстън

Екипът на Торквато показа, че този модел има връзка с хипотеза на Риман, която казва, че простите числа следват модел, тясно свързан с дзета - функцията на Риман.

Хипотезата може и да е вярна - но много математици, често настроени не толкова романтично, казат, че е прекалено красива, за да е вярна. И вече 160 години, откакто Риман я представи за пръв път, никой не успя да я докаже, въпреки че Институтът Клей дава един милион долара за това. (може да прочетете повече тук „Хипотезата на Риман за лаици”).

Настоящото изследване използва теорията на числата, за да изгради теоретичната основа на своите числени експерименти. Изследователите осъзнават, че макар простите числа да се появяват случайно в кратки интервали, за по-дълги участъци от числовата линия може да се намери закономерност в иначе привидно хаотичните позиции на простите числа.

Екипът откри точни индикации на такъв модел, използвайки компютърни симулации, за да види какво ще се случи, ако простите числа се разглеждат като низ от атоми, подложени на рентгеново лъчение.

Откритието на изследователите може да помогне както в областта на математиката, така и в науката за материалите. "Простите числа са с красиви структурни свойства, включително и неочакван ред, хипереднаквост и ефективно гранично-периодично поведение", заяви Торквато. „Простите числа ни помагат да проучим това ново състояние на материята”.

"Очарователното на това изследване е, че ни дава различна перспектива на простите числа: вместо да ги разглеждате като числа, можем да ги видим като частици и да се опитаме да очертаем техния модел (структура) чрез рентгенова дифракция", обяснява Хенри Кон (Henry Cohn), главен изследовател в Microsoft Research, неучаствал в проучването.