Карен Кескула Уленбек бе удостоена с наградата Абел 2019 за пионерната си работа в областта на геометрията, анализа, математическата физика и др. Наградата Абел се присъжда всяка година за изключителни научни постижения в математиката. Уленбек е първата жена в 16-годишната история на наградата, която я получава.
Работата на Уленбек обхваща зашеметяващ набор от области. "Нейната сила е в голямата широта на работата и интересите ѝ", отбелязва Саймън Доналдсън (Simon Donaldson), носител на медала "Фийлдс" от 1986 г. за работа, която включва някои от идеите на Уленбек. "Голяма част от нейната работа има истинско пионерно”.
Ето някои от проблемите, върху които е работила Уленбек, представени от математическото издание на Харвард Plus magazine.
Мехурчетата
Една новаторска нишка в творчеството на Уленбек започва с нещо изненадващо познато: фактът, че най-краткият път между две точки в равнината е права линия.

Най-краткият път между A и B върви по права линия. Как би могло да бъде иначе? Всеки друг път е очевидно по-дълъг!
Повечето от нас просто приемат този факт за даденост - как би могло да бъде иначе? - но също така е възможно да се докаже и с математическа точност. За всеки път, свързващ двете точки има формула, която ни дава дължината (някои знаят - формулата е интеграл). С малко манипулации може да намерите пътя, който минимизира тази формула. Това доказателство принадлежи към една област, наречена на вариационно смятане, която се свежда до минимизиране или максимизиране на някои величини като се отчитат ограниченията.
Добавяйки едно измерение, подобен проблем ни въвлича в красивия свят на сапунните филми. Играчките, които използваме за издухване на сапунени мехурчета, идват с пластмасов пръстен, който се потапя в сапунена вода. Сапуненият филм, който се образува в рамката след потапянето, има възможно най-малка площ. На теория може да си представите, че филмът е с всякакви форми, той може да има подутини например, но плоската форма минимизира площта и съответно повърхностното напрежение и енергията - природата обича да бъде пестелива.

Преди да издуем мехурчетата, сапунът образува филм, обхващащ пластмасовата рамка (или в този случай всяка от двете рамки!). Снимка: fir0002, CC.
За математик това поставя очевидно предизвикателство - като се има предвид относителната лекота, с която може да се намери най-късия път между две точки в равнината, може ли да се намери и повърхността с минимална площ, произведена от дадена рамка? Всъщност, в математиката повърхността се смята за минимална, не само ако може да се направи с помощта на една голяма рамка, но и ако във всяка точка се начертае рамка на тази повърхност, така че ако се потопи тази рамчица в сапунена вода, нейният филм да се съгласува с повърхността - цялата повърхност ще се състои от малки минимални повърхнини. Какъвто и метод да открием, минималната повърхнина трябва да работи не само в един конкретен пример, но и в пълната си съвкупност
Намирането на минимални повърхности е изключително труден проблем. До 19-ти век са известни само три от тях: равнината, катеноидът и хеликоидът.

Хеликоид. Снимка © The Exploratorium.

Катеноид.
В преследване на минималното
Уленбек завършва докторската си дисертация по вариационно смятане през 1966 г. и насочва вниманието си към минималните повърхнини, когато се запознава с Джонатан Сакс (Jonathan Sacks) през 70-те години. "Не знаех много за минималните повърхнини, но говорихме за тях и работихме заедно," разказва Уленбек в интервю за Сelebratio през 2018 г. с Алин Джаксън (Allyn Jackson). "Той внесе познанията си за предмета на минималните повърхнини и аз внесох основната идея [на работата]."
Един от начините за определяне на минимална повърхност, с който е по-лесно да се работи, отколкото с площ, е нещо, наречено енергия (вж. по-долу за формули). Точно както дължината на пътя между две точки може да бъде описана с интеграл, така може да се опише и енергията на повърхнината. Задачата е да се намери повърхнина, която минимизира тази формула на енергията.
Когато се занимаваме само с пътища, проблемът е сравнително ясен. Изключително полезен факт (при обсъждането на Уленбек и Сакс) е, че пътеките могат да се събират, приближавайки се по-близо и по-близо един до друг, докато накрая се слеят (конвергират) към граничния път.
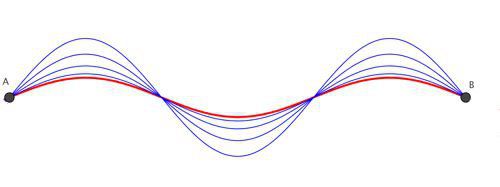
Илюстрация на сини пътища, конвергиращи към червения път. Може да си представите безкрайно много повече сини пътища, които се приближават по-близо до червения.
Концепцията за енергията е тясно свързана с това сближаване (конвергенция): ако в рамките на колекция от гладки пътища от А до В енергията на всеки път е по-малка от някаква граница, тогава може да бъдете сигурни, че колекцията съдържа последователност от пътища, които клонят към непрекъснат граничен път от А до В. Тъй като главният проблем е да се определи минималния път от безкрайния брой на всички пътища, свързващи А и В, не е изненадващо, че този вид резултат на компактност (наречен компактен, защото има граници) е важен.
Когато става въпрос за повърхнини обаче енергията не е достатъчно силна, за да ви даде подобен резултат. Проблемът е в многото начини, по които може да се опише повърхнината. Представете си повърхнина, която изглежда като деформирана сфера; например един картоф или спукана футболна топка. За да намерим пътя си по такава неприятна повърхнина, можем да построим карта от кръгла сфера: всяка точка на кръглата сфера е свързана с точка на деформираната сфера. Именно точно това правим, когато представяме Земята, която е малко по-различна от идеална сфера с карта на глобус. Има обаче много различни начини да се изберат точките на сферата, които да се свържат към точка на повърхнината, така че има много различни избори на картата.

Сферата може да служи като карта на повърхността на картофа, ако всяка точка x върху картофа се свърже с точка и сферата. Има обаче много различни възможности за избор как да се свържат точките, така че има много различни карти.
Пертурбации на енергията
В математическия свят на Уленбек и Сакс, повърхнини в 3D пространството (или всяко друго многообразие) също са описани с определени видове карти. В този контекст формулата, която ни дава енергията на повърхнината, не е задължителна за вида на картата, която използваме, по-специално, тя не показва разстоянията. Когато става въпрос за последователности от карти обаче мащабът може да бъде важен - той може да обърка конвергенцията на картите и следователно да ни лиши от вида на компактността, който ни трябва да покажем, че съществуват минимални повърхнини.
Игра с енергията
За две компактни многообразия M и N и гладка карта от M до N , енергията E на картата се дава от формулата:
 |
където | ∇u | е стандартната норма, определена от метриката на TM x и TN {u (x)}.
Леко вариращите енергийни изрази, които Уленбек и Сакс разглеждат, имат формулата
 |
за α > 1.
В една забележителна статия, Уленбек и Сакс намират изобретателен начин за решаване на този проблем. Те се опитват да подобрят обичайния израз за енергията на повърхнината, за да получат изрази, които са малко по-различни. Тези нови изрази могат да отразят мащаба и следователно покажат тежестта, за да докажат най-компактния резултат. Това означава, че за всяко от тези леко различни изрази може да се намери значима минимизираща карта. Може да се конструират поредица от леко различни енергийни изрази, които са схождат с оригиналния енергиен израз. Всеки от тези леко различни изрази идва със собствена минимизираща карта, така че идеята е да се види дали тези минимизиращи карти се схождат с нещо смислено по отношение на изходния израз за енергията.
Последователността минимизиращи карти може да не е сходима в някои точки от сферата, върху която са построени, но такива точки са краен брой и все още е възможно да се опише какво се случва там - като се мащабират картите в малките области около неудобните точки, се открива, че областите се „взривяват” от нещо, което може да се нарече "мехурчета" на повърхностите, които картите описват. Можете да научите повече в отличната статия на Саймън Доналдсън (Simon Donaldson) за работата на Уленбек.

Схема на картиране на мехурче - малки области около една неудобна точка се „взривяват” в мехурчета. Илюстрация от Notices of the American Mathematical Society.
Тази идея, наречена от Уленбек „основна“, за премащабиране на задачата, позволява на Уленбек и Сакс да докажат важни резултати за съществуването на минимални повърхности. Тя намира приложения и в много други проблеми. "Много задачи са напълно геометрични [не се интересуват от мащаба]", обяснява Уленбек в интервюто си с Джаксън. "Ако имате задача, когато търсите метрика, и така или иначе, няма свойствен външен мащаб, можете наистина да промените мащаба, който разглеждате."
Отвъд сапунените мехури
Идеите на Уленбек и Сакс създадоха голяма част от последващата работа в няколко области. "[Тяхната] работа за минималните повърхнини е основата за по-нататъшното развитие на много области в продължение на четири десетилетия", отбелязва Доналдсън. Удивително е, че едно такова направление включва област от физиката, която е далеч отвъд сапунените мехури: опитът да се създаде теория за всичко, която не само описва явленията, които можем да видим, но и обяснява света в много малки и много големи мащаби, които никога няма да видим.
Както Уленбек отбелязва, "никой не е играл с квантови ефекти като дете", така че концепциите, включени тук, не са толкова интуитивни, колкото са сапунените мехури. Но съществуват математически прилики между теорията на минималните повърхности и квантовата физика, описани от така наречената калибровъчна теория. "Мощна математическа специфика е това, че интуицията и техниките могат да се прехвърлят между теорията на минималните повърхности и калибровъчната теория", пише Уленбек.
Уленбек насочва вниманието си към теорията, която е в основата на нашето разбиране за физиката на частиците, наречена теория на Янг-Милс. Уленбек е пионер в изучаването на уравненията на Янг-Милс от строга математическа гледна точка, откривайки феномени като образуване на мехури и понятия за компактност в процеса. Нейната работа в тази област постави основите на всяка следваща работа в калибровъчната теория. Нейната работа по инстантоните е също вдъхновена от проблемите на физиката, но в крайна сметка революционизира чистата математика и води до основен учебник, написан с Дан Фрийд. (на български: "Полето на Янг-Милс", "Когато бозоните на Янг-Милс изядоха бозоните на Голдстоун")
Изследването на калибровъчната теория, първоначално „осиновено дете” на математиката (както го нарече Уленбек), не само е облагодетелствало физиците, но и от своя страна се връща обратно в чистата математика. Това е доведе до резултати, които може би никога не биха настъпили без физическото вдъхновение.
"Определено съм много привлечена от идеята, че има много различни аспекти в математиката и виждам връзките," каза Уленбек в интервюто си с Джаксън. "Бих се заинтересувала да науча много повече за нещата, които не са основно математика, но са свързани с други области с математиката".
Дотук споменахме много малко от постиженията на Уленбек - да ѝ пожелаем късмет с преследването на все още неразкритите връзки между физиката и математиката.