В забележителната си работа от 1952 г. английският математик Алън Тюринг въвежда понятие, което става известно като патерн (модел, мотив с определена закономерност) на Тюринг - идеята, че ако бъде нарушена динамиката на някои хаотични еднородни системи, това може да породи стабилни подредени модели.
Подобен „ред от хаоса“ или самоорганизация се превръща в теоретична основа за обяснението на всякакви странни, повтарящи се мотиви (патерни), наблюдавани в природата.
Това е толкова добра теория, че десетилетия по-късно учените все още откриват забележителни примери за нея на необичайни и екзотични места - реални патерни на Тюринг в ситуации, които самият Тюринг никога не е имал възможност да види.
Последното въплъщение на този теоретичен феномен се оказват "вълшебните" кръгове (fairy circles) - мистериозни образувания сред пустинните треви, които растат около отчетливо кръгли петна от суха почва, документирани за първи път през 1971 г. в пустинята Намиб в Южна Африка.
Сега се знае, че се срещат и в Ангола, Южна Африка, Австралия. Те достигат от 2 до 15 метра в диаметър. Вътре в загадъчните петна нищо не расте.
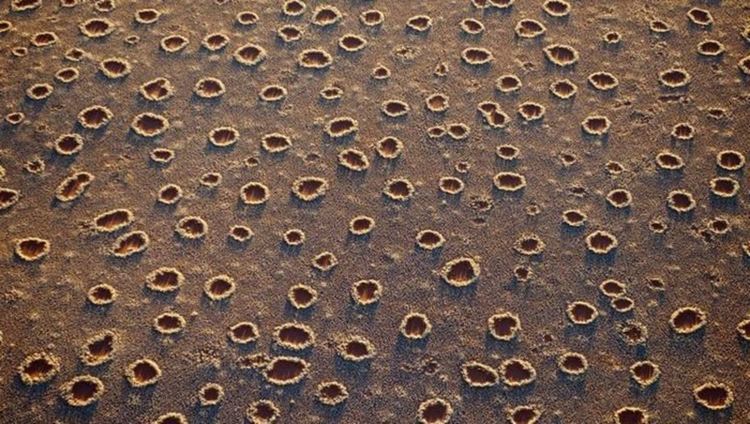
 Изображение от дрон на австралийски "вълшебни" кръгове (fairy circles). Кредит: Stephan Getzin/University of Göttingen
Изображение от дрон на австралийски "вълшебни" кръгове (fairy circles). Кредит: Stephan Getzin/University of Göttingen
Обясненията за тяхното съществуване варират от митични до най-обикновени и допреди няколко години все още се спореше за техния произход. В началото някои предполагаха, че странните кръгове се дължат на дейността на термитите под африканската почва.
По-правдоподобна е хипотезата, че феноменът се дължи на силната конкуренция на тревите за жизненоважни ресурси като вода и хранителни вещества в сурова и суха среда.
Това означава, че явлението е още един пример в природата за патерна на Тюринг. Но емпиричните доказателства, подкрепящи хипотезата, са недостатъчни, защото физиците, занимаващи се моделиране на динамиката на Тюринг, рядко провеждат полеви тестове в пустинята в подкрепа на своите идеи.
„Съществува силен дисбаланс между теоретичните вегетационни модели, техните прогнози и оскъдността на емпирични доказателства, че моделираните процеси са правилни от екологична гледна точка“, се коментира в новата статия, публикувана в списание Journal of Ecology, на екип, ръководен от еколога Стефан Гецин (Stephan Getzin) от Университета в Гьотинген, Германия .
За да преодолеят тази липса, Гецин и неговият екип отиват на място, близо до миньорския град Нюман в региона Пилбара, Западна Австралия, и с помощта на дронове, оборудвани с мултиспектрални камери, изследват вълшебните кръгове отгоре.
Според една от хипотезите на екипа, патерните на Тюринг ще са по-изразени при тревите с по-голяма зависимост от влагата.
Използвайки сензори за влага за проверка на състоянието на почвата, екипът установява, че по-жизнените треви систематично по-често се проявяват вълшебни кръгове, отколкото тревите с ниска жизненост.
Това означава, че за първи път разполагаме с емпирични данни, които да подсказват, че вълшебните кръгове са следствие на теорията на Тюринг от десетилетия.
"Интригуващото е, че тревите активно проектират собствената си среда, като формират симетрично разположени модели на празни петна", коментира Гецин.
"Растителността се възползва от допълнителните води, осигурени от големите вълшебни кръгове, и така поддържа сухата екосистема функционална дори в много сурови и сухи условия. Без самоорганизацията на тревите тази област вероятно ще стане пустиня, доминирана от безплодна почва."
Според изследователите тревите, съставляващи полетата с вълшебните кръгове, растат заедно в сътрудничество, преобразявайки средата си, за да се справят по-добре в условията на почти вечната суша.
„Чрез формирането на периодични патерни от празни петна, растителността се възползва от допълнителния воден ресурс, осигурен от вълшебните кръгове", обясняват авторите, "и по този начин екосистемата се поддържа функционална при по-ниски стойности на валежите в сравнение с равномерната растителност“.
Справка: Bridging ecology and physics: Australian fairy circles regenerate following model assumptions on ecohydrological feedbacks
Stephan Getzin, Todd E. Erickson, Hezi Yizhaq, Miriam Muñoz‐Rojas, Andreas Huth, Kerstin Wiegand
First published: 21 September 2020, Journal of Ecology. DOI: https://doi.org/10.1111/1365-2745.13493
Източник: Mysterious Circles in The Desert Explained by Alan Turing Theory From 70 Years Ago
За Алън Тюринг и леопардовите петна
Един от най-популярните примери на модела на Тюринг отговаря на детския въпрос "Защо се появяват петната и ивиците по кожите на някои животни?
Това е удивителен по своята красота природен процес.
Окраската често служи за маскировка и тъй като има определена роля за оцеляването на вида, тази информация се предава по наследство. Леопардовите петна, например, не са идентични за всеки екземпляр от този вид, но въпреки това са ясно различими от тигровите.
 Първият опит да се отговори на този въпрос е на Алън Тюринг, прародител на всички компютърни науки и пионер в областта на изкуствения интелект. На този изключителен учен е посветен филма "Игра на кодове".
Първият опит да се отговори на този въпрос е на Алън Тюринг, прародител на всички компютърни науки и пионер в областта на изкуствения интелект. На този изключителен учен е посветен филма "Игра на кодове".
Всъщност, Тюринг не се е интересувал пряко от механизма, определящ окраската на животните, а по-скоро от законите на химичните и биопроцеси в неравновесните системи.
Т.н.реактивна дифузия е може би най-простият случай на система, която не се намира в равновесие. Това е химическа реакция, която протича в определен обем, от който продуктите на реакцията могат да дифузират (да се разпространяват) в околната среда. Ако липсваше тази дифузия, продуктите от реакцията ще останат в този обем и постепенно ще се разпределят равномерно и хомогенно в него и това разпределение ще остане стабилно.
Тюринг установил какво ще бъде разпределението на продуктите на реакцията в същия обем, ако те могат постепенно да излизат навън. В този случай продуктите на реакцията се разпределят в обема по различен начин: в някои точки са повече, а в други - по-малко. При това картината на редуващите се сгъстявания и разреждания зависи от скоростта на реакцията и скоростта на дифузията.
Това редуване на сгъстяване и разреждане се нарича "модели на Тюринг", а механизмът на образуването им - "pattern formation" , формиране на патерни. Трудно може да се намери аналог на български на тази дума, тя може да се преведе приблизително като модел, образец, шаблон, десен, тапет, шарки, но във всички тези случаи смисълът й ще бъде осакатен. Патерн означава закономерна регулярност (подреденост).
Подобни модели се използват в изкуството, архитектурата, дизайна като в повторението на елементите се търси определен ефект върху зрителя, а понякога са следствие от условия на технологична ефективност. Пример за патерн са и тухлените стени, плочките, мозайките.
Петната върху кожата на леопардите и другите животни са само част от многобройните примери за патерни, които дава природата - симетрии, фрактални структури, спирали, меандри, вълни, пяна, пукнатини. Всички те имат различни механизми на образуване, затова нека се върнем към случаите на реактивна дифузия.
Най-простият случай на патерн се появява в система, където реакцията включва само два агента, единият от които е "активатор", който стимулира образуването на второто вещество и "инхибитор" - който потиска активността на първия.
Какъв е механизмът, който определя за едни животни точки, за други - по-големи петна, а за трети - ивици?
 |
 |
 |
Дейвид Юнг доразвива идеята на Тюринг на базата на клетъчните автомати.
 Още в ранния зародиш кожата на леопарда (или тигъра, зебрата, жирафа и т.н.) се покрива с равномерно с меланоцити (клетки пигмент). Тези клетки могат да са в едно от двете състояния:
Още в ранния зародиш кожата на леопарда (или тигъра, зебрата, жирафа и т.н.) се покрива с равномерно с меланоцити (клетки пигмент). Тези клетки могат да са в едно от двете състояния:
- различаваща се (D) и
- неразличима (U).
Цветът се произвежда само в D-клетките. Освен това, D-клетките отделят два морфогена:
- активатор (A) и
- инхибитор (I) - обратното на активатор.
Двата химикала се разпръскват от всяка D-клетка и тяхната концентрация намалява с отдалечаване от D-клетката.
А-концентрацията е най-голяма около D-клетката, но отслабва по-бързо от I-концентрацията. Така на известно разстояние от D-клетката, I-концентрацията започва да превишава А-концентрацията от тази клетка.
Всяка клетка постоянно се изпълва с А и I морфогени от всички съседни D-клетки. Ако в U-клетката, А-концентрацията превишава I-концентрацията, клетката става D и започва сама да отделя морфогени. Ако в D- клетката, I-концентрацията превишава А-концентрацията, клетката става U и престава да произвежда морфогени.
Счита се, че еволюцията на окраската на животинските кожи е форма на самоорганизация на D-клетките и произтича от току-що описаните химически цикли.

Дейвид Юнг представя модела на кожата на животното като квадратен масив от клетки меланоцити в едно от двете състояния:
- жива (за различаваща се D-клетка) и
- мъртва (за неразличима U-клетка).
Приема се, че морфогенното разсейване има форма на кръг. който има радиус, например 6 клетки. Всяка D-клетка в границите на този кръг отделя морфогени, които достигат централната клетка. Ако D-клетката е достатъчно близо до центъра (да кажем в пределите на кръг с радиус 3 от центъра), тогава тя внася А-морфогени в централната клетка. Всяка D-клетка на разстояние повече от 3 от центъра (но все пак не далече от 6) внася I-морфогени в централната клетка. Юнг приема А-концентрацията за единица, константа за всички D-клетки в радиус 3 от центъра, а за I-концентрацията - някакво друго число w, константа за всички D-клетки в пръстеновидната област между 3 и 6 от центъра.
След това се действа по правилото на клетъчните автомати: преброяваме всички D-клетки в този пръстен и наричаме това число ID, преброяваме всички D-клетки в кръга с радиус 3 и наричаме това число AD.
Ако AD - w*ID > 0 централната клетка става D (различаваща се),
Ако AD - w*ID < 0 централната клетка става U (неразличима),
Ако AD - w*ID = 0 централната клетка остава без промени.
 |
 |
 |
Благодарение на този механизъм, за да се предава по наследство окраската на кожата е необходимо да се предава само специфичната за вида концентрация на инхибитора.

Вероятно по същия механизъм се образуват шарките не само на бозайниците. Забележете тялото на морския охлюв на снимката вдясно. Не повтарят ли точно симулацията по-горе за w=0.13?
Тюринг публикува изследванията си през 1952г., но първото експериментално потвърждение на идеите му става през 1998г. Следват серия от други доказателства и днес статията Тюринг вече се е превърнала в класика. На нея се позовават не само химици и физици, но и много биолози, които изучават подобни процеси у живите същества и то не само процесите, водещи до появата на ивици или петна. Те са само частен случай на по-общ процес.
"Ако има два процеса, които действат [като активатор и инхибитор], винаги може да получите като резултат периодични модели", казва Джереми Грийн (Jeremy B.A. Green), биолог-изследовател, съавтор на публикацията Periodic stripe formation by a Turing-mechanism operating at growth zones in the mammalian palate. Той и колегите му са установили, че две химически вещества, които се държат като активатор и инхибитор, водят до равномерно разположени набраздявания в устата в миши ембриони. Когато изследователите увеличават или намаляват активността на тези химикали, моделът се променя точно както предсказват уравненията на Тюринг .
Моделът на Тюринг описва всякакъв растеж на биологичните системи, при които размножаващите се на едно място клетки се разпространяват (дифузират) в съседните области. Такива процеси водят, както показват проучванията, до появата подобни на Тюринговите модели.
Източници:
Fractal Geometry - Yale University